Pred strelo se moramo dobro zaščititi. Zato moramo poznati njene fizikalne lastnosti in načine, na katere se te lastnosti kažejo v naravi ter v naših bivalnih in industrijskih okoljih. Tako so zelo pomembna dolgoletna opazovanja in meritve, ki omogočajo najprimernejše dimenzioniranje obrambnih mehanizmov pred učinki strele.

Najpomembnejši podatki o razelektritvenem procesu so: temenska ali amplitudna vrednost razelektritvenega toka v (kA), naboj toka strele Q v (As), strmina toka strele v (kA/µs), kvadratni impulz toka strele ∫i² · dt v (A²s), čas trajanja toka strele v (s), valovna upornost kanala strele v (Ω) in število udarov na nekem območju.

 Temenska vrednost razelektritvenega toka

Z vidika zaščite pred strelo je seveda najpomembnejša vrednost velikost razelektritvenega toka, saj ta teče prek naprav zaščite objekta in s svojimi vzporednimi potmi tudi po kovinskih delih samega objekta. Kot smo omenili, je lahko tok strele posledica pozitivnega ali negativnega naboja. Negativni udari strele tvorijo razelektritvene valove, ki se po obliki zelo razlikujejo med seboj. Čas trajanja njihovega čela prvega udarnega vala znaša od 10 do 15 µs. Že pri drugi zaporedni razelektritvi je njihovo čelo krajše in hrbet vala nekoliko daljši. Tudi temenska vrednost drugega vala je ponavadi manjša.

Pozitivni razelektritveni valovi se navadno pojavljajo z enim razelektritvenim valom, ki traja od 0,1 do 0,2 s. Njihov čas trajanja čela je relativno dolg in znaša od 20 do 50 µs. Temenske vrednosti pozitivnih razelektritvenih valov lahko dosežejo tudi več kakor 1.000 kA.

Preglednica 2.6.1.1: Največje temenske vrednosti razelektritvenih tokov z verjetnostjo pojavnosti

Verjetnost, da bodo določene temenske vrednosti presežene, je prikazana na naslednji preglednici 2.6.2.

Temenske vrednosti razelektritvenih tokov se ob različnih udarih seveda pojavljajo v različni velikosti in lahko njihovo pričakovanje obravnavamo le na podlagi določene verjetnosti, ki izvira iz predhodnih opazovanj. Tako so te vrednosti prikazane v naslednji preglednici 2.6.1 za štiri zaščitne nivoje, ki so jim nato prilagojene štiri vrste konstrukcijskih izvedb rešitev zaščite pred strelo.

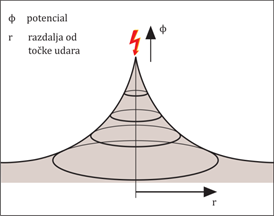
Preglednica 2.6.1.2: Najmanjše temenske vrednosti razelektritvenih tokov z verjetnostjo pojavnosti

Električni razelektritveni tok na svoji poti naleti na prevodne dele, ki niso idealni prevodniki. Na njih se zaradi ohmske upornosti pojavi napetostni padec z značilno obliko potencialnega lijaka, ki ga kaže slika 2.6.1.1.

Potencial se izračuna iz enostavne oblike:

U = I · R

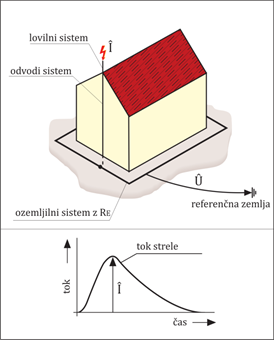
Slika 2.6.1.1: Porazdelitev potencialov ob atmosferski razelektritvi pri odvajanju toka v homogeno zemljišče

Naslednja slika 2.6.1.2 prikazuje udarni razelektritveni tok, ki se razelektri prek strelovodnega lovilnika in ustvarja potencialno razliko glede na oddaljeno referenčno zemljo.

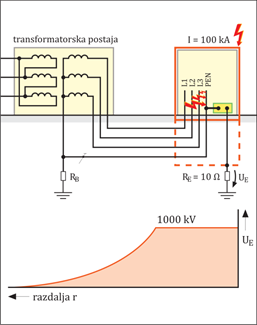
Slika 2.6.1.3: Prikaz potenciala do referenčne zemlje pri odvajanju udarnega razelektritvenega toka

Upornost ozemljilnega sistema je skladno z evropskimi standardi priporočena v vrednosti 10 Ω. Pri razelektritvenem toku strele 100 kA bi pri tej ozemljilni upornosti nastal napetostni padec 1.000 kV. Pri tako visoki napetosti bi vsekakor, če ne bi uporabili ustreznih zaščitnih ukrepov, prišlo do električnega preboja na druge inštalacije. Primer takega pojava je prikazan na sliki 2.6.1.4.

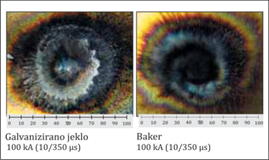
Slika 2.6.1.4: Preboj izolacije v električno inštalacijo zaradi porasta napetosti ob odvajanju razelektritvenega toka

 Naboj razelektritvenega toka

Povprečna skupna količina naboja, ki se sprosti ob atmosferskih razelektritvah, znaša okoli 10 C. Pri močnih razelektritvah pa se sprosti tudi 300 C nabranega razelektritvenega naboja. Električni naboj računamo:

 Q =∫i · dt

Količina naboja, ki se sprosti ob razelektritvi, odloča o nastali energiji, ki se v točki udara spremeni v toploto. Ta nastala toplotna energija zadostuje, da se stali del kovine v točki udara in lahko posledično zažge vnetljivi material, ki se te točke dotika. Obratovalna praksa pozna številne takšne primere. Konkreten primer na pločevini iz galvaniziranega jekla in bakra je prikazan na sliki 2.6.2.1.

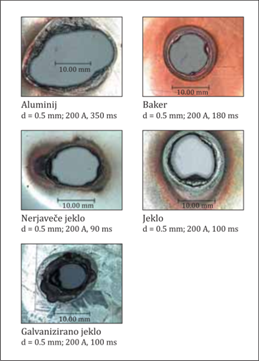
Slika 2.6.2.1: Učinek preskusnega toka z udarnim valom 100 kA (10/350 µs)

Na sliki 2.6.2.2 je za pločevine iz standardnih materialov pločevinastih streh z debelino 0,5 mm prikazan učinek taljenja posameznih kovin pri električnem toku 200 A v času 100 ms.

Slika 2.6.2.3: Preluknjana pločevina zaradi učinkov taljenja kovine

Zaradi taljenja tankih pločevin je treba pri dimenzioniranju pločevinastih streh, ki jih želimo uporabiti za del strelovodne lovilne mreže, vendar imajo pod seboj vnetljive materiale, ustrezno povečati debelino pločevine. Če tega ni mogoče upoštevati, je treba tanko pločevinasto streho opremiti z dodatno lovilno mrežo.

Glede na veljavni standard SIST EN 62305-1 je pri projektiranju treba upoštevati za različne zaščitne nivoje naslednje vrednosti celotnih razelektritvenih nabojev:

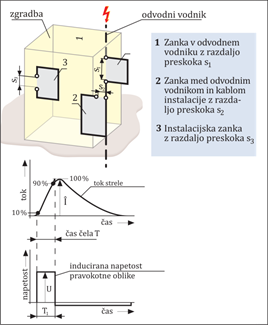
Strmina razelektritvenega toka strele

Tok strele v atmosferskem razelektritvenem procesu ima obliko tokovnega impulza. Tok zelo hitro doseže svojo največjo vrednost, ki pa se nato počasi zmanjšuje. To je posledica potrebnega prodora toka skozi prostor, ki v svojem začetku potrebuje velik napetostni in nabojni zagon, da premaga zračni kanal, po katerem se lahko izenači z nasprotno naelektrenim polom na zemlji. Okoliščine nastanka, v bistvu elektrostatičnih neravnotežij med kapacitivno porazdeljenimi naboji in ustvarjanjem njihovega naravnega ravnotežja, so odvisne od prirodnih naključnih vremenskih razmer in njihove geometrije. Zato se tudi ob različnih razelektritvah toki strele na njihovem čelu impulza ne spreminjajo vedno enako. Nekateri toki naraščajo hitreje, nekateri pa počasneje. Za tiste toke strele, ki se v začetku spreminjajo zelo hitro, pravimo, da imajo veliko strmino.

Strmino toka strele označujemo s s in jo obravnavamo kot prirast toka v določenem času s = ∆i/∆t oziroma še natančneje s = di/dt. Njena merska enota je A/S ali kA/µs.

Zaradi hitrega spreminjanja strmine porasta tokovnega impulza v okolici poti, po kateri teče tak razelektritveni tok, nastajajo močna elektromagnetna polja. Hitrim spremembam toka sledijo nato visoke inducirane napetosti, ki so mnogo višje od nazivnih obratovalnih napetosti, s katerimi delujejo naprave v objektu, v katerega je udarila strela. Na sliki 2.6.3.1 so prikazane tri inštalacijske zanke, med katerimi se na določenih mestih vodniki zanke ali priključne sponke naprav približajo na preskočne razdalje (s_1, s₂ in s₃) in zaradi tega nastane električni preboj.

Na sliki je prikazana inducirana napetost pravokotne oblike, kar bi ustrezalo spremembi toka strele ∆i/∆t. Za dejansko spremembo di/dt bi se inducirana napetost pojavila v obliki impulza z veliko večjo amplitudno vrednostjo.

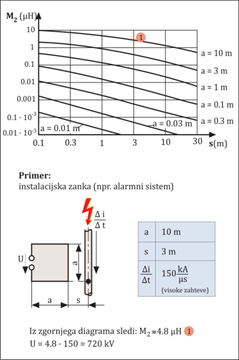
Slika 2.6.3.1: Inducirane napetosti v različnih vrstah zank na objektu pri spremembi električnega toka

V konkretnih primerih v praksi je zelo pomembno, kolikšna površina zanke je odprta in na razpolago prodiranju spremenljivega magnetnega polja. Od tega je odvisna dejanska inducirana napetost v sami zanki, ki je odvisna od medsebojne induktivnosti med zanko in vodnikom, ki prevaja razelektritveni tok strele. Medsebojna induktivnost je za nekatere zanke v obliki kvadrata prikazana na sliki 2.6.3.2 v odvisnosti od razdalje od strelovodnega odvoda. Na isti sliki je izračunana tudi inducirana napetost za kvadratno zanko s stranico kvadrata a = 10 m in razdaljo 3 m od strelovodnega odvoda. Za izračun je vzeta enačba za inducirano napetost:

 U = M · ∆i/∆t

Za računanje v realnih razmerah bi seveda morali upoštevati natančnejšo obliko za spremembo porasta toka strele, in sicer:

 U = M · di/dt

Tako bi amplitudna vrednost imela še večjo vrednost, kar pomeni, da je tudi v realnosti njen udar še nevarnejši za uničenje naprav v okolici vodnikov, ki prevajajo tok strele. No, sreča je, da se tok strele ponavadi razdeli po več vzporednih vodnikih, kar nekoliko olajša razmere.

Slika 2.6.3.2: Inducirana napetost pravokotnega vala v zanki pri spremembi toka strele ∆i/∆t

Kot je razvidno s slike, je upoštevana strmina toka strele ∆i/∆t v višini 150 kA/µs, kar je sorazmerno velika vrednost. Tako je tudi izračunana inducirana napetost 720 kV zelo visoka. Ob upoštevanju diferencialne spremembe toka v času pa bi bila temenska vrednost udara še večja.